[翻譯] An Overview of ResNet and its Variants
2019/10/02
// 2019/10/09 完成翻譯初稿。
-----
After the celebrated victory of AlexNet [1] at the LSVRC2012 classification contest, deep Residual Network [2] was arguably the most groundbreaking work in the computer vision/deep learning community in the last few years. ResNet makes it possible to train up to hundreds or even thousands of layers and still achieves compelling performance.
-----
暨 LSVRC2012 分類競賽中 AlexNet [1] 完勝之後,深度殘差網絡 [2] 可說是過去幾年裡,計算機視覺 / 深度學習社群的代表作。 ResNet 可訓練數百甚至數千層的網路,而且維持最高水準。
-----
Taking advantage of its powerful representational ability, the performance of many computer vision applications other than image classification have been boosted, such as object detection and face recognition.
-----
利用其強大的表現能力,除了圖像分類以外,還提高了許多計算機視覺應用程式的性能,例如物件檢測和人臉辨識。
-----
Since ResNet blew people’s mind in 2015, many in the research community have dived into the secrets of its success, many refinements have been made in the architecture. This article is divided into two parts, in the first part I am going to give a little bit of background knowledge for those who are unfamiliar with ResNet, in the second I will review some of the papers I read recently regarding different variants and interpretations of the ResNet architecture.
-----
自從 ResNet 在 2015 年引起人們的關注以來,學術界中的許多人都深入探討,並改善其架構。 本文分為兩個部分,在第一部分中,我將為不熟悉 ResNet 的人提供一些背景知識,在第二部分中,我將復習我最近閱讀的一些文章,這些文章涉及不同 ResNet 體系結構的變體和解釋。
-----
Revisiting ResNet
-----
According to the universal approximation theorem, given enough capacity, we know that a feedforward network with a single layer is sufficient to represent any function. However, the layer might be massive and the network is prone to overfitting the data. Therefore, there is a common trend in the research community that our network architecture needs to go deeper.
-----
根據通用逼近定理,給定足夠的容量,我們知道具有單層的前饋網絡足以表示任何功能。 但是,該層可能很龐大,並且網絡傾向於過度擬合數據。 因此,研究社群有一個共同的趨勢,那就是我們的網路架構需要更深。
-----
Since AlexNet, the state-of-the-art CNN architecture is going deeper and deeper. While AlexNet had only 5 convolutional layers, the VGG network [3] and GoogleNet (also codenamed Inception_v1) [4] had 19 and 22 layers respectively.
-----
自從 AlexNet 以來,最先進的 CNN 架構越來越深。 雖然AlexNet僅具有 5 個卷積層,但 VGGNet [3] 和 GoogleNet(也代號為Inception_v1)[4] 分別具有 19 和 22 層。
-----
However, increasing network depth does not work by simply stacking layers together. Deep networks are hard to train because of the notorious vanishing gradient problem — as the gradient is back-propagated to earlier layers, repeated multiplication may make the gradient infinitively small. As a result, as the network goes deeper, its performance gets saturated or even starts degrading rapidly.
-----
但是,僅通過將層堆疊在一起,無法增加網路深度。 由於惡名昭彰的梯度消失,難以訓練深層網路隨著梯度向後傳播到較淺的層,連乘可能會使梯度無限小。 結果,隨著網路不斷加深,其性能將達到飽和甚至開始迅速下降。
-----
Fig. 1. Increasing network depth leads to worse performance.
-----
Before ResNet, there had been several ways to deal the vanishing gradient issue, for instance, [4] adds an auxiliary loss in a middle layer as extra supervision, but none seemed to really tackle the problem once and for all.
-----
在 ResNet 之前,有幾種方法可以解決消失的梯度問題,例如 [4] (GoogLeNet)在中間層添加輔助損失作為額外的監督,但似乎沒有一種方法能夠一勞永逸地真正解決該問題。
-----
The core idea of ResNet is introducing a so-called “identity shortcut connection” that skips one or more layers, as shown in the following figure:
-----
ResNet 的核心思想是引入一個跳過一層或多層的所謂「恆等捷徑」,如下圖所示:
-----
Fig. 2. A residual block.
-----
The authors of [2] argue that stacking layers shouldn’t degrade the network performance, because we could simply stack identity mappings (layer that doesn’t do anything) upon the current network, and the resulting architecture would perform the same. This indicates that the deeper model should not produce a training error higher than its shallower counterparts. They hypothesize that letting the stacked layers fit a residual mapping is easier than letting them directly fit the desired underlaying mapping. And the residual block above explicitly allows it to do precisely that.
-----
[2](ResNet v1)的作者認為,堆疊層不應降低網路性能,因為我們可以簡單地在當前網路上堆疊單位映射(不執行任何操作的層),並且最終的架構也可以執行相同的操作。 這表明,較深的模型不應產生比其較淺的模型更高的訓練誤差。 他們假設讓堆疊的層擬合殘差映射比讓它們直接擬合所需的底圖更容易。 上面的殘差塊明確允許它精確地做到這一點。
-----
As a matter of fact, ResNet was not the first to make use of shortcut connections, Highway Network [5] introduced gated shortcut connections. These parameterized gates control how much information is allowed to flow across the shortcut. Similar idea can be found in the Long Term Short Memory (LSTM) [6] cell, in which there is a parameterized forget gate that controls how much information will flow to the next time step. Therefore, ResNet can be thought of as a special case of Highway Network.
-----
Fig. 3. The ResNet architecture.
-----
實際上,ResNet 並不是第一個使用「捷徑」的模型,Highway Network [5] 引入了「閘道捷徑」。 這些參數化的門,控制流過「捷徑」的訊息量。 在長的短期記憶(LSTM)[6] 單元中可以找到類似的想法,在該單元中有一個參數化的「忘記門」,該門控制著將有多少信息流向下一個時間點。 因此,可以將 ResNet 視為 Highway 的特例。
-----
However, experiments show that Highway Network performs no better than ResNet, which is kind of strange because the solution space of Highway Network contains ResNet, therefore it should perform at least as good as ResNet. This suggests that it is more important to keep these “gradient highways” clear than to go for larger solution space.
但是,實驗表明,Highway 的性能並不比 ResNet 好,這很奇怪,因為 Highway 的解空間包含 ResNet,因此其性能至少應與 ResNet 一樣好。 這表明保持這些“梯度公路”的通行性比尋求更大的解空間更重要。
-----
Following this intuition, the authors of [2] refined the residual block and proposed a pre-activation variant of residual block [7], in which the gradients can flow through the shortcut connections to any other earlier layer unimpededly. In fact, using the original residual block in [2], training a 1202-layer ResNet resulted in worse performance than its 110-layer counterpart.
-----
遵循這種直覺,[2](ResNet v1)的作者改進了殘差塊並提出了殘差塊的預激活變體 [7](ResNet v2),其中,梯度可以無阻礙地流過「捷徑」而到達任何其他較淺的層。 實際上,使用文獻 [2](ResNet v1)中的原始殘差塊,訓練 1202 層的 ResNet 會比 110 層的 ResNet 表現差。
-----
Fig. 4. Variants of residual blocks.
-----
The authors of [7] demonstrated with experiments that they can now train a 1001-layer deep ResNet to outperform its shallower counterparts. Because of its compelling results, ResNet quickly became one of the most popular architectures in various computer vision tasks.
[7](ResNet v2)的作者通過實驗證明,他們現在可以訓練 1001 層深的 ResNet 來勝過其較淺的 ResNet。 由於其出色的結果,ResNet 迅速成為各種電腦視覺任務中最受歡迎的模型之一。
-----
Recent Variants and Interpretations of ResNet
-----
As ResNet gains more and more popularity in the research community, its architecture is getting studied heavily. In this section, I will first introduce several new architectures based on ResNet, then introduce a paper that provides an interpretation of treating ResNet as an ensemble of many smaller networks.
-----
隨著 ResNet 在研究界越來越受歡迎,其架構讓很多人投入研究。 在本節中,我會先介紹幾種基於 ResNet 的新架構,然後介紹一篇論文,它解釋為何 ResNet 可視為許多較小網路的組合。
-----
ResNeXt
-----
Xie et al. [8] proposed a variant of ResNet that is codenamed ResNeXt with the following building block:
-----
Xie et al. [8] 提出了一個 ResNet 的變體,其代號為 ResNeXt,其結構如下:
-----
Fig. 5. Left: a building block of [2], right: a building block of ResNeXt with cardinality = 32.
-----
This may look familiar to you as it is very similar to the Inception module of [4], they both follow the split-transform-merge paradigm, except in this variant, the outputs of different paths are merged by adding them together, while in [4] they are depth-concatenated. Another difference is that in [4], each path is different (1x1, 3x3 and 5x5 convolution) from each other, while in this architecture, all paths share the same topology.
-----
你可能會覺得這很熟悉,因為它與 [4](GoogLeNet)的 Inception 模組很像,它們都遵循 split-transform-merge 範式,除了在此變體中,不同路徑的輸出通過將它們加在一起來合併,而在 [4](GoogLeNet)它們是深度級聯的。 另一個區別是,在 [4](GoogLeNet)中,每個路徑都互不相同(1x1、3x3 和 5x5 卷積),而在此架構中,所有路徑共享相同的拓撲。
-----
The authors introduced a hyper-parameter called cardinality — the number of independent paths, to provide a new way of adjusting the model capacity. Experiments show that accuracy can be gained more efficiently by increasing the cardinality than by going deeper or wider. The authors state that compared to Inception, this novel architecture is easier to adapt to new datasets/tasks, as it has a simple paradigm and only one hyper-parameter to be adjusted, while Inception has many hyper-parameters (like the kernel size of the convolutional layer of each path) to tune.
-----
作者介紹了一個稱為基數的超參數-獨立路徑的數量,以提供一種調整模型容量的新方法。 實驗表明,通過增加基數,可以比通過更深入或更廣泛地提高精度。 作者指出,與 Inception 相比,這種新穎的架構更容易適應新的數據集 / 任務,因為它具有簡單的範式並且僅需調整一個超參數,而 Inception 具有許多超參數(例如內核大小)。 每個路徑的捲積層)進行調整。
-----
This novel building block has three equivalent form as follows:
-----
這種新穎的組件具有以下三種等效形式:
-----
Fig. 6. RexNeXt.
-----
In practice, the “split-transform-merge” is usually done by pointwise grouped convolutional layer, which divides its input into groups of feature maps and perform normal convolution respectively, their outputs are depth-concatenated and then fed to a 1x1 convolutional layer.
-----
實際上,「拆分轉換合併」通常是通過逐點分組卷積層完成的,將其輸入分為特徵圖組並分別執行一般卷積,將其輸出進行深度級聯,然後餵到 1x1 卷積層。
-----
Densely Connected CNN
-----
Huang et al. [9] proposed a novel architecture called DenseNet that further exploits the effects of shortcut connections — it connects all layers directly with each other. In this novel architecture, the input of each layer consists of the feature maps of all earlier layer, and its output is passed to each subsequent layer. The feature maps are aggregated with depth-concatenation.
-----
Huang et al. [9] 提出了一種稱為 DenseNet 的新穎架構,進一步利用了快捷連接的效果-將所有層彼此直接連接。 在這種新穎的價構中,每一層的輸入均由所有較早層的特徵圖組成,並且其輸出將傳遞到每個後續層。 特徵圖通過深度級聯聚合。
-----
Fig. 7. DenseNet.
-----
Other than tackling the vanishing gradients problem, the authors of [8] argue that this architecture also encourages feature reuse, making the network highly parameter-efficient. One simple interpretation of this is that, in [2][7], the output of the identity mapping was added to the next block, which might impede information flow if the feature maps of two layers have very different distributions. Therefore, concatenating feature maps can preserve them all and increase the variance of the outputs, encouraging feature reuse.
-----
除了解決消失的梯度問題外,[8] 的作者認為,這種架構還鼓勵特徵重用,從而使網路具有更高的參數效率。 一個簡單的解釋是,在[2] [7]中,將「捷徑」的輸出添加到下一個塊,如果兩層的特徵圖具有非常不同的分佈,則可能會阻礙信息流。 因此,級聯特徵圖可以保留它們全部並增加輸出的方差,從而鼓勵特徵重用。
-----
Fig. 8. DenseNet.
-----
Following this paradigm, we know that the l_th layer will have k * (l-1) + k_0 input feature maps, where k_0 is the number of channels in the input image. The authors used a hyper-parameter called growth rate (k) to prevent the network from growing too wide, they also used a 1x1 convolutional bottleneck layer to reduce the number of feature maps before the expensive 3x3 convolution. The overall archiecture is shown in the below table:
-----
遵循此範例,我們知道第 l_層將具有 k *(l-1)+ k_0 個輸入特徵圖,其中 k_0 是輸入圖像中的通道數。 作者使用了稱為增長速率(k)的超參數來防止網路增長得太寬,他們還使用了 1x1 卷積瓶頸層來減少特徵圖的數量,然後才進行昂貴的 3x3 卷積。 總體架構如下表所示:
-----
Fig. 9. DenseNet architectures for ImageNet.
-----
Deep Network with Stochastic Depth
-----
Although ResNet has proven powerful in many applications, one major drawback is that deeper network usually requires weeks for training, making it practically infeasible in real-world applications. To tackle this issue, Huang et al. [10] introduced a counter-intuitive method of randomly dropping layers during training, and using the full network in testing.
-----
儘管 ResNet 已被證明在許多應用上功能強大,但一個主要缺點是,較深的網路通常需要幾週的時間去訓練,使其在實際應用上幾乎不可行。 為了解決這個問題,Huang et al. [10] 介紹了一種違反直覺的方法,即在訓練過程中隨機丟棄各層,並在測試中使用完整的網路。
-----
The authors used the residual block as their network’s building block, therefore, during training, when a particular residual block is enable, its input flows through both the identity shortcut and the weight layers, otherwise the input only flows only through the identity shortcut. In training time, each layer has a “survival probability” and is randomly dropped. In testing time, all blocks are kept active and re-calibrated according to its survival probability during training.
-----
作者使用殘差塊作為其網路的構建塊,因此,在訓練期間,啟用特定殘差塊後,其輸入將流過「恆等捷徑」和權重層,否則輸入僅流過恆等捷徑」。 在訓練時,每一層都有一個「生存概率」,並且被隨機丟棄。 在測試期間,所有模塊都保持活動狀態,並根據其在訓練期間的生存概率進行重新校準。
-----
Formally, let H_l be the output of the l_th residual block, f_l be the mapping defined by the l_th block’s weighted mapping, b_l be a Bernoulli random variable that be only 1 or 0 (indicating whether a block is active), during training:
-----
正常,在訓練期間,假設 H_l 為第 l 個殘差塊的輸出,f_l 為第 l 個塊的加權映射定義的映射,b_l 為僅 1 或 0(表示一個塊是否處於活動狀態)的伯努利隨機變數:
-----

Formula 1.
-----
When b_l = 1, this block becomes a normal residual block, and when b_l = 0, the above formula becomes:
-----
當 b_l = 1 時,此塊成為正常殘差塊,而當 b_l = 0 時,上式變為:
-----
Formula2.
-----
Since we know that H_(l-1) is the output of a ReLU, which is already non-negative, the above equation reduces to a identity layer that only passes the input through to the next layer:
-----
由於我們知道 H_(l-1) 是 ReLU 的輸出,而它已經是非負的,因此上述等式簡化為僅將輸入傳遞到下一層的恆等層:
-----

Formula 3.
-----
Let p_l be the survival probability of layer l during training, during test time, we have:
-----
令 p_l 為訓練過程中 l 層的生存概率,在測試期間,我們有:
-----
Formula4.
-----
The authors applied a linear decay rule to the survival probability of each layer, they argue that since earlier layers extract low-level features that will be used by later ones, they should not be dropped too frequently, the resulting rule therefore becomes:
-----
作者將線性衰減規則應用於每一層的生存概率,他們認為,由於較早的層會提取供以後的層使用的初級特徵,因此不應將它們太頻繁丟棄,因此,得出的規則變為:
-----

Formula 5.
-----
Where L denotes the total number of blocks, thus p_L is the survival probability of the last residual block and is fixed to 0.5 throughout experiments. Also note that in this setting, the input is treated as the first layer (l = 0) and thus never dropped. The overall framework over stochastic depth training is demonstrated in the figure below.
-----
其中 L 表示塊的總數,因此 p_L 是最後一個剩餘塊的生存概率,並且在整個實驗中固定為 0.5。 另請注意,在此設置中,輸入被視為第一層(l = 0),因此永遠不會丟失。 下圖展示了隨機深度訓練的總體框架。
-----
Fig. 10. During training, each layer has a probability of being disabled.
-----
Similar to Dropout [11], training a deep network with stochastic depth can be viewed as training an ensemble of many smaller ResNets. The difference is that this method randomly drops an entire layer while Dropout only drops part of the hidden units in one layer during training.
-----
與 Dropout [11] 類似,訓練具有隨機深度的深層網路可以看作是訓練許多較小的 ResNet 的集合。 不同之處在於,此方法隨機丟棄整個圖層,而 Dropout 在訓練過程中僅將一層中的部分隱藏單元丟棄。
-----
Experiments show that training a 110-layer ResNet with stochastic depth results in better performance than training a constant-depth 110-layer ResNet, while reduces the training time dramatically. This suggests that some of the layers (paths) in ResNet might be redundant.
-----
實驗表明,與固定深度 110 層的 ResNet相比,訓練隨機深度的 110 層 ResNet 可獲得更好的性能,同時顯著減少了訓練時間。 這表明 ResNet 中的某些層(路徑)可能是多餘的。
-----
ResNet as an Ensemble of Smaller Networks
-----
[10] proposed a counter-intuitive way of training a very deep network by randomly dropping its layers during training and using the full network in testing time. Veit et al. [12] had an even more counter-intuitive finding: we can actually drop some of the layers of a trained ResNet and still have comparable performance. This makes the ResNet architecture even more interesting as [12] also dropped layers of a VGG network and degraded its performance dramatically.
-----
[10] 提出了一種反直覺的方式來訓練非常深的網絡,方法是在訓練過程中隨機捨棄某些層,並在測試時使用整個網絡。 Veit et al. [12] 有一個更違反直覺的發現:我們實際上可以刪除經過訓練的 ResNet 的某些層,並且仍然具有可比的性能。 這使 ResNet 架構變得更加有趣,因為 [12] 也丟棄了 VGGNet 的各個層並顯著降低了其性能。
-----
[12] first provides an unraveled view of ResNet to make things clearer. After we unroll the network architecture, it is quite clear that a ResNet architecture with i residual blocks has 2 ** i different paths (because each residual block provides two independent paths).
-----
[12] 首先提供了一個清晰的 ResNet 視圖,以使事情更加清晰。 在我們展開網絡體系結構之後,很明顯,具有 i 個殘差塊的 ResNet 架構具有 2 ** i 個不同的路徑(因為每個殘差塊提供兩條獨立的路徑)。
-----
Fig. 11.
-----
Given the above finding, it is quite clear why removing a couple of layers in a ResNet architecture doesn’t compromise its performance too much — the architecture has many independent effective paths and the majority of them remain intact after we remove a couple of layers. On the contrary, the VGG network has only one effective path, so removing a single layer compromises this one the only path. As shown in extensive experiments in [12].
-----
鑑於上述發現,很明顯,為什麼在 ResNet 架構中刪除幾層並不會過多地影響其性能 — 該架構具有許多獨立的有效路徑,而在我們刪除了幾層後,大多數路徑仍保持不變。 相反,VGGNet 只有一條有效路徑,因此刪除單個層會損害這條唯一路徑。 如 [12] 中廣泛的實驗所示。
-----
The authors also conducted experiments to show that the collection of paths in ResNet have ensemble-like behaviour. They do so by deleting different number of layers at test time, and see if the performance of the network smoothly correlates with the number of deleted layers. The results suggest that the network indeed behaves like ensemble, as shown in the below figure:
-----
作者還進行了實驗,以顯示 ResNet 中的路徑集合具有類似集合的行為。 他們通過在測試時刪除不同數量的層來做到這一點,並查看網路性能是否與刪除的層數平滑相關。 結果表明該網路的行為確實像集合體,如下圖所示:
-----
Fig. 12. error increases smoothly as the the number of deleted layers increases.
-----
Finally the authors looked into the characteristics of the paths in ResNet:
-----
最後,作者研究了 ResNet 中路徑的特徵:
-----
It is apparent that the distribution of all possible path lengths follows a Binomial distribution, as shown in (a) of the blow figure. The majority of paths go through 19 to 35 residual blocks.
-----
很明顯,所有可能路徑長度的分佈都遵循二項式分佈,如 blow figure 的(a)所示。 大多數路徑經過 19 到 35 個殘差塊。
-----
Fig. 13.
-----
To investigate the relationship between path length and the magnitude of the gradients flowing through it. To get the magnitude of gradients in the path of length k, the authors first fed a batch of data to the network, and randomly sample k residual blocks. When back propagating the gradients, they propagated through the weight layer only for the sampled residual blocks. (b) shows that the magnitude of gradients decreases rapidly as the path becomes longer.
-----
研究路徑長度與流經路徑的梯度大小之間的關係。 為了獲得長度為 k 的路徑中梯度的大小,作者首先將一批數據饋入網路,並隨機採樣 k 個殘差塊。 當反向傳播梯度時,它們僅針對採樣的殘差塊傳播通過權重層。 (b)表明,隨著路徑變長,梯度的大小會迅速減小。
-----
We can now multiply the frequency of each path length with its expected magnitude of gradients to have a feel of how much paths of each length contribute to training, as in (c). Surprisingly, most contributions come from paths of length 9 to 18, but they constitute only a tiny portion of the total paths, as in (a). This is a very interesting finding, as it suggests that ResNet did not solve the vanishing gradients problem for very long paths, and that ResNet actually enables training very deep network by shortening its effective paths.
-----
現在,我們可以將每個路徑長度的頻率乘以其預期的梯度大小,以感覺到每個長度的路徑對訓練有貢獻,如(c)所示。 令人驚訝的是,大多數貢獻來自長度為 9 至 18 的路徑,但它們僅佔總路徑的一小部分,如(a)所示。 這是一個非常有趣的發現,因為它表明 ResNet 不能解決很長路徑的消失梯度問題,而 ResNet 實際上可以通過縮短有效路徑來訓練非常深的網路。
-----
In this article, I revisited the compelling ResNet architecture, briefly explained the intuitions behind its recent success. After that I introduced serveral papers that propose interesting variants of ResNet or provide insightful interpretation of it. I hope it helps strengthen your understanding of this groundbreaking work.
-----
Conclusion
-----
在本文中,我重新介紹了引人注目的 ResNet 架構,並簡要解釋了其近期成功背後的直觀。 之後,我介紹了幾篇論文,這些論文提出了 ResNet 的有趣變體或提供了有見地的解釋。 我希望它有助於加深您對這項開創性工作的理解。
-----
All of the figures in this article were taken from the original papers in the references.
本文中的所有圖均來自參考文獻中的原始論文。
-----
References
# 本篇翻譯的來源文章
An Overview of ResNet and its Variants – Towards Data Science
https://towardsdatascience.com/an-overview-of-resnet-and-its-variants-5281e2f56035
[1]. A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems,pages1097–1105,2012.
[2]. K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. arXiv preprint arXiv:1512.03385,2015.
[3]. K. Simonyan and A. Zisserman. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:1409.1556,2014.
[4]. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed, D. Anguelov, D. Erhan, V. Vanhoucke, and A. Rabinovich. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition,pages 1–9,2015.
[5]. R. Srivastava, K. Greff and J. Schmidhuber. Training Very Deep Networks. arXiv preprint arXiv:1507.06228v2,2015.
[6]. S. Hochreiter and J. Schmidhuber. Long short-term memory. Neural Comput., 9(8):1735–1780, Nov. 1997.
[7]. K. He, X. Zhang, S. Ren, and J. Sun. Identity Mappings in Deep Residual Networks. arXiv preprint arXiv:1603.05027v3,2016.
[8]. S. Xie, R. Girshick, P. Dollar, Z. Tu and K. He. Aggregated Residual Transformations for Deep Neural Networks. arXiv preprint arXiv:1611.05431v1,2016.
[9]. G. Huang, Z. Liu, K. Q. Weinberger and L. Maaten. Densely Connected Convolutional Networks. arXiv:1608.06993v3,2016.
[10]. G. Huang, Y. Sun, Z. Liu, D. Sedra and K. Q. Weinberger. Deep Networks with Stochastic Depth. arXiv:1603.09382v3,2016.
[11]. N. Srivastava, G. Hinton, A. Krizhevsky, I. Sutskever and R. Salakhutdinov. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. The Journal of Machine Learning Research 15(1) (2014) 1929–1958.
[12]. A. Veit, M. Wilber and S. Belongie. Residual Networks Behave Like Ensembles of Relatively Shallow Networks. arXiv:1605.06431v2,2016.









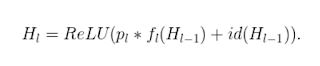




No comments:
Post a Comment