AI 三部曲(深度學習:從入門到精通)
2019/05/02
前言:
本文試著整理出十篇 Deep Learning(深度學習)的論文,作為初學者進入深度學習的第一關。內容包含 CV(電腦視覺)五篇、NLP(自然語言處理)五篇。如果是完全的初學者,建議可以先看一下 AI 從頭學 [23]。
-----
Fig. Penrose Triangle(圖片來源:Pixabay)。
-----
Summary:
Deep Learning 兩個主要的應用領域是 CV 與 NLP。
首部曲:
CV 三個重要主題則是 CNN(卷積神經網路)、Semantic Segmentation(語意分割)、Object Detection(物件偵測)。CNN 是 Deep Learning 的基礎 [1],最重要的幾個模型是 LeNet [2]-[4]、NIN [5]、ResNet [6]-[8]。Semantic Segmentation 則以 FCN 為代表 [9]。Object Detection 則可以從 YOLOv1 開始 [10]。
NLP 建議的閱讀順序是 LSTM [11]、Seq2seq [12]、Attention [13]、ConvS2S [14]、Transformer [15]。以上是 BERT 的主要基礎,BERT 是一個 NLP 預訓練模型,於 2018 年底推出,在許多 NLP 任務中的表現都很好 [16]。
以上十篇是深度學習的基礎。另有 Optimization [17]、Regularization [18]、Normalization [19]、Semantic Segmentation [20]、Object Detection [21]、Word2vec [22] 等主題可以深入。
二部曲:
假定這十篇論文已經可以充分掌握,我推薦用 Python 實作一下 LeNet [24]。然後是三個重要主題:Regularization 如 Weight Decay 或 Dropout、Optimization 如 Momentum 或 Adam、Normalization 如 Batch 或 Layer [25]。若對 Deep Learning 有極大的興趣,可以在上述主題都熟練後,重新打一下機器學習(其實就是數學)的基礎 [26], [27]。
三部曲:
NLP 如果要徹底掌握 BERT,其實要回頭複習 NNLM、Word2vec、GloVe、fastText、ELMo、AWD-LSTM、ULMFiT、OpenAI GPT [29]。
以上主題十分龐大,建議還是以這十篇的 LeNet [2], [23] 開始。說的誇張一點,LeNet 如果搞定,Deep Learning 就可以算是掌握九成了,其他都是變化。
-----
Outline
CNN(卷積神經網路)的演變
一、LeNet(The Net)
◎ Regression(迴歸)
◎ LeNet
◎ Convolution(卷積)
◎ Neuron(神經元)
◎ Pooling(池化)
◎ Full Connection Layer(全連接層)
◎ Linearly Non-separable(線性不可分)
◎ Linearly Separable(線性可分)
◎ Activation Function(激活函數)
◎ Gradient Descent(梯度下降法)
◎ Back Propagation(反向傳播法)
二、NIN(Network in Network)
◎ NIN(網路中的網路)
◎ 1 x 1 Convolution(1x1 卷積)
三、ResNet(Residual Net)
◎ Residual Structure(殘差結構)
◎ ResNet(殘差網路)
四、FCN(Fully Convolutional Network)
◎ Semantic Segmentation(語意分割)
◎ FCN(全卷積網路)
◎ Up Sampling(上取樣)
五、YOLOv1
◎ Object Detection(物件偵測)
◎ YOLO(你只能看一次)
◎ Loss Function(YOLO 的損失函數)
六、LSTM(Long Short-Term Memory)
◎ RNN(遞迴神經網路)
◎ LSTM(長的短期記憶)
七、Seq2seq(Sequence to Sequence)
◎ Seq2seq(序列到序列)
八、Attention
◎ Attention(注意力)
九、ConvS2S(Convolutional Seq2seq)
◎ ConvS2S(卷積的序列到序列)
十、Transformer
◎ Transformer(變形金剛)
◎ Query、Key、Value
◎ Self Attention(自注意力)
◎ Qd、Ke、Ve(編碼端的 QKV)
◎ Qd、Kd、Vd(解碼端的 QKV)
-----

Fig. 1. CNN(卷積神經網路)的演變 [1]。
-----
CNN(卷積神經網路)的演變
-----
正文開始之前,先說說 CNN 的歷史 [1]。
1998 的 LeNet 是第一個里程碑。簡單說就是可以辨識 0 到 9 的阿拉伯數字,並且已經用在美國的一些銀行。不過由於當然電腦運算量的限制,沈寂了一段很長的時間。
2012 的 AlexNet 是第二個重要的里程碑。今年是 2019,在這段時間內,藉著 GPU 龐大的運算能力,2013 的 ZFNet、NIN,2014 的 VGGNet、GoogLeNet,到 2015 的 ResNet,影像辨識能力一舉超越人類專家。
簡單說,ResNet = LeNet + NIN + LSTM。這四篇論文,在本篇文章中會陸續介紹。
-----
一、LeNet(The Net)
-----
CNN是個有點複雜的概念,因此,在介紹 LeNet 之前,我們先以一個相對簡單的迴歸分析,作為熱身。
-----
Fig. 2. Regression(迴歸)[2]。
-----
◎ Regression(迴歸)
-----
什麼是迴歸?以圖二為例,左邊是一個線性迴歸,中間接近一個二次的拋物線,右邊是高次的曲線。
這三個模型,哪一個是對的?哪一個最好,其實沒有一定。但一般說來,我們不希望模型的誤差太大,也不希望模型太複雜,所以中間這張圖,就是一般我們所需要的。
藉由有限的資料,找出一個函數來 fit 這些資料。函數找出來以後,就可以用 x 來預測 y。比方說,預測股市(有這麼簡單嗎?哈哈)。
-----
Fig. 3. LeNet [2]。
-----
◎ LeNet
-----
圖二是個迴歸模型,可以用 x 預測 y。圖三是 LeNet,CNN 模型,可以用一張 32x32 的圖片,預測圖片的數字是 0 到 9 的機率,總和為 1。
你可以理解的是迴歸模型的輸入是一個點 x,輸出是一個 y 值。LeNet 的 輸入是 1024 個點,x0 到 x1023,輸出是一個 y 向量,y0 到 y9,y0 到 y9 的總和為 1。
丟進模型的,也沒有限定是阿拉伯數字。以圖三為例,如果你把 A 丟進訓練好的 LeNet 下去運算,你可能認為 4 的可能是是 0.1,9 的可能性是 0.1,其他的可能性均為 0,但是正規化之後,4 和 9 的可能性都是 0.5,其他還是 0。
LeNet 的結構是 輸入層、卷積層、池化層、卷積層、池化層、全連接層、全連接層、輸出層。輸入層就是 1024 個點,輸出層就是10 個 0 到 1 的實數且總和為 1。
下面繼續介紹卷積層、池化層、以及全連接層。
-----
Fig. 4. Convolution(卷積)[2]。
-----
◎ Convolution(卷積)
-----
卷積是什麼呢?圖四是一個平面上,或者叫空間(二維)上的卷積。
不過我們先來說一下時間上的卷積,這邊會有一點信號與系統以及數位訊號處理的觀念。
讓我們直接進入數位訊號處理。假定有一個 x + 1 的信號,與一個 x + 1 的信號(或者一個 x + 1 的信號通過一個 x + 1 的系統),兩個信號作卷積,得出來的就是一個 (x + 1)*(x + 1) 的信號,也就是 x^2 + 2x + 1 的信號。所以一維的卷積,你當成多項式相乘就可以了。
卷積的觀念從一維推廣到二維,如圖四,就是一個小矩陣通過一張較大的圖片。每一個點旁邊有八個點,共九個點。每個矩陣也有九個值,你可以想成用你的朋友來重新定義你這個人,比方說旁邊都是紅點,那你這九個人基本上就是紅,旁邊都是綠點,那你這九個人基本上就是綠、旁邊都是藍點,那你這九個人基本上就是藍。至於實際運算,可以參考一維的運算方式。
在數位信號處理上,這個 3x3 的矩陣叫做空間濾波器,不同的濾波器有不同的功能,比方說有些對垂直線敏感,有些對水平線敏感。這些都是由專家找出來的。深度學習跟數位訊號處理最大的差距,就是在深度學習中,矩陣的權重是靠資料訓練出來的。
如何訓練,後面的梯度下降法會仔細說明。
-----
Fig. 5. Neuron(神經元)[2]。
-----
◎ Neuron(神經元)
-----
神經元由一些元素構成,分別是輸入、權重、偏置、激活函數、輸出。
圖五可以跟圖四一起看。比方說 x11 到 x33 這九個原圖上的點,就是輸入。矩陣上的 w11 到 w33 就是對應的權重。相乘再加總之後,如果大於一個 bias(偏置,圖五漏掉了),被激活了,就繼續經過一個 activation function(激活函數)計算,然後輸出。如果沒有被激活,那輸出就是 0。常見的激活函數有 sigmoid、tanh、ReLU 等。
激活函數有一個功能是壓縮資料,另一個更重要的功能是增加模型的表現力(所以都是非線性),激活函數如何影響到神經網路,後面的線性可分與線性不可分會說明。
跟 weight 一樣,bias 也是靠訓練得到的。
-----
Fig. 6. Pooling(池化)[2]。
-----
◎ Pooling(池化)
-----
池化有兩個功能,一是降維(或者叫壓縮資料、減少資料),一是保留特徵。主要有最大值池化跟平均池化。
-----
Fig. 7. Full Connection Layer(全連接層)[4]。
-----
◎ Full Connection Layer(全連接層)
-----
經過卷積、池化、卷積、池化之後,LeNet 會有兩個全連接層。全連接層主要就是線性組合(另外還要加上激活函數的非線性)。
如果以 LeNet 為例,第一層卷積層主要功能是找出各個角度的直線,第二層卷積層則是將一些小直線拼成垂直線、水平線、斜線、或曲線。接下來的全連接層則是將第二層的物件組成一個數字。
為什麼在 CNN 前幾層會用到卷積層,而不是全連接層呢?主要是影像的特性,每個點只會跟鄰近的點有關連,跟遠方的點,基本上是不相干的。所以用一些小矩陣,把影像的特徵提取出來。
-----
Fig. 8. Linearly Non-separable(線性不可分)[4]。
-----
◎ Linearly Non-separable(線性不可分)
-----
圖八是一個線性不可分的例子。
-----
Fig. 9. Linearly Separable(線性可分) [4]。
-----
◎ Linearly Separable(線性可分)
-----
透過數層的非線性激活函數,線性不可分就變成線性可分了。
-----
Fig. 10. Activation Function(激活函數)[4]。
-----
◎ Activation Function(激活函數)
-----
不同的激活函數,都有可能將線性不可分轉為線性可分。
-----
Fig. 11. Gradient Descent(梯度下降法)[2]。
-----
◎ Gradient Descent(梯度下降法)
-----
接下來是深度學習的重頭戲,梯度下降法 [2]。
我們先一一由左至右解釋符號。
Wk 是本次的權重,Wk-1 是上次的權重。epsilon 是步長,偏微分符號(讀做 round),E(W) 是 error function,或者叫做 cost function,是預測值跟實際值的誤差。
利用圖二中左邊第一個點來說明。先想像你的預測值跟實際值的呈現如一座山,你想要讓誤差值變小,也就是下山,你能怎麼做?可以往右踏一步,也可以往左踏一步,如果你往左踏一步,發現高度有下降一點點,就是正確的方向,那你只要反覆一直走,就可以下山。
epsilon 就是步長,Wk-1 就是上一次的位置,Wk 就是新的位置,導數為正,斜率值大於零,表示遞增,這時你的 x 座標要減去一個正值,也就是向左移,誤差就會變小,也就是下山。
網路函數,變數為 x,常數為 w。可是當你想要調整權重,這時要固定 x。至於為何是偏微而不是常微,因為 w 有很多要調整。
這邊會有遇到局部最小值的可能,有些方法可以解決,譬如 momentum [17]。
-----
Fig. 12. Back Propagation(反向傳播法)[3]。
-----
◎ Back Propagation(反向傳播法)
-----
BP
1. S 是訓練集,有 M 個樣本。L 是總層數。o 是一個樣本,y 是該樣本 o 的值。 2. 隨機設定所有 w 和 b 的初始值。 3. 做到收斂或做到指定的次數。 4. 選擇一個小批次 O。 5. 把 O 丟進前向網路。 6. 得到 V,跟實際值 Y 有差距,為 E。 7. 將 E 代入 G。 8. 從最後一層開始往前做。 9. 計算 w 的梯度。 10. 計算 b 的梯度。 11. 更新 w。 12. 更新 b。 13. 權重轉置乘上 G 代入前一層的 E。 14. 如果不是第一層,則 15. 取激活函數 f 的微分值,與 E 做 hadamard product 再代入 G。 16. end if。 17. end for。 18. end while 19. 傳回 DNN 裡,所有層裡面的 w 和 b。 20. end procedure。
以上先簡單註解圖十二演算法二十行,再仔細說明內容。
一、背景:
反向傳播法其實就是微積分裡的 chain rule,一個函數的導數,可以分解成其隱含數導數的乘積。神經網路由於是由一連串的激活函數跟線性組合構成,所以神經網路的導數,可以分解成一連串 f' 與 w 的連續乘積 [7], [8]。
二、上標與下標:
上標 L 是代表神經網路的第 L 層,下標 t 則是代表 time,Wt 是本次的權重,Wt+1 則是更新後的權重。
三、輸出
V 是輸出,演算法第六行,因為 cost function 是 (1/2)(V - Y)^2,所以其導數是 E = V - Y。第七行的 G 則是暫存。
四、W 和 b
第九行的 W 比第十行的 b,多乘一個 V,是因為 V[l] = f(WV[l-1]+b),原本 V 是變數,但是要更新 W 和 b 時,W 和 b 變成變數,V 變成常數。以 b 為變數,WV[l-1] 是常數,在 chain rule 微分後不見了。以 W 為變數,WV[l-1] 微分後會留下 V[l-1]。
五、chain rule
第十三到第十五行,則是把導數傳到前一層,暫存的 G,乘上 f' 跟 W,即可得到前一層的導數,f' 在這邊是要利用網路裡暫存的數值,用電腦算出來的。
小結:
BP 把每層的導數 f' 跟 w 層層展開。 梯度下降法藉由調整權重讓損失函數的值朝 0 前進。損失函數 L 是 輸出 V 的函數。輸出函數 V 是激活函數 F 的函數。激活函數 F 是神經元 Z 的函數。神經元 Z 是 W X + B 的函數。以上是反向傳播。更新 W 時,變數由 X 變為 W,所以導數要多乘一個 X 項。更新 B 時,變數由 X 變為 B,不用多乘 W 跟 X,因為 W 與 X 在此都是常數,微分後就不見了!
經過層層的更新 W 和 b 的權重,最後傳回,一次更新網路。
-----
二、NIN(Network in Network)
-----
Fig. 13. NIN(網路中的網路)[5]。
-----
◎ NIN(網路中的網路)
-----
圖十三,NIN,就是在兩個卷積層之間,再插入一個叫 MLPconv 的網路。
-----
Fig. 14. 1 x 1 Convolution(1x1 卷積) [5]。
-----
◎ 1 x 1 Convolution(1x1 卷積)
-----
簡單說,就是千層派的概念。64 張特徵圖,可以壓扁成 32 張特徵圖。當然,也可以擴充為 128 張特徵圖。每張新的特徵圖,都是由原來的 64 張特徵圖,以不同的權重構成,權重值?靠訓練 [5]。
這邊的 1 x 1 convolution,或稱為 conv1,其實跟我們一般概念上的 conv3 或 conv5 不同。conv3 是空間上的卷積,conv1 則是 channel 間的卷積。所謂 channel,64 張 feature maps,就是 64 個 channel,新的特徵圖上,每一個點 xij,都是不同 channel 上,所有不同的 xij 的線性組合。
精神跟空間的卷積還是一樣,平面上的像素跟鄰近的像素相關性高,channel 間的相關性,同樣位置的每一點相關性高。
Conv1 由於可以有效壓縮資料,在目前的深度學習中,已是基本配備。
-----
三、ResNet(Residual Net)
-----
Fig. 15. Residual Structure(殘差結構)[6]。
-----
◎ Residual Structure(殘差結構)
-----
圖十五是一個殘差結構,也就是在原來的網路架構上,多加了一個 identity(或者叫 skip connection),這樣餘下的部分,就變成 F(x) 這個殘差部分。
殘差網路比原來網路的值小,所以對變化比較敏感,也比較好訓練。而從 LSTM 概念來的 identity 則可以減低深度網路梯度消失的問題 [7]。
-----
Fig. 16. ResNet(殘差網路)[6]。
-----
◎ ResNet(殘差網路)
-----
截至本次更新日期,2019/07/01,《Deep residual learning for image recognition》這篇論文被引用 24409 次,獲得極大的成功。不過你大概可以說,ResNet = LeNet + NIN + LSTM。偉大的論文,有時只是很基本的元素,加上卓越的洞見。
這邊可以先簡單再回顧一下 CNN 的歷史 [1]。
1998 LeNet 是一個不錯的網路,但當時受限於計算機的運算力有限,所以網路大小也受限。
2012 AlexNet 有了 GPU 跟一些新技巧,加深了網路,大幅提升網路性能。
2013 ZFNet 微調 AlexNet,改善一點點。
2013 NIN 讓加深網路更可行。
2014 VGGNet 用兩個 conv3 組成一個 conv5,反覆加深,到 16 層結果很棒,19 比 16 好一點點,22 以上反而更差。這表示加深網路並不是萬靈丹。
2014 GoogLeNet 除了大量使用 conv1,也多了兩個輔助輸出,可以直接傳遞梯度到網路比較前面的部分。
2015 的 ResNet 跟 Highway Networks 都採用 LSTM 的 identity 概念,不過 ResNet 比較簡潔,也做了比較多實驗。結果大獲成功,陸續也有更多的變形。
不過,後續的研究,則說明,ResNet 除了可以減低梯度消失的問題,更大的可能是避免模型退化,也就是神經元無法輸出,或者兩個神經元輸出一樣 [6]。
-----
四、FCN(Fully Convolutional Network)
-----
Fig. 17. Semantic Segmentation(語意分割)[9]。
-----
◎ Semantic Segmentation(語意分割)
-----
一般 CNN 的功能是辨識一張圖片的內容為何,譬如阿拉伯數字 0 到 9,如圖三。
FCN 則是能夠分辨到像素級別,譬如圖十七。每個屬於貓的像素,都被塗上棕色,每個屬於狗的像素,都被塗上紫色,背景則是綠色。
-----
Fig. 18. FCN(全卷積網路)[9]。
-----
◎ FCN(全卷積網路)
-----
怎麼做到呢?圖十八上,在一般的 CNN 中,最後是全連接層,輸出可能是三十種類別的可能性,取最大的那個當作結果。
FCN 最後不用全連接層,基本上還是卷積層,所以最後是三十張特徵圖。每個像素穿過這三十張特徵圖,取最大值那張所屬的類別,作為此像素的類別。
-----
Fig. 19. Up Sampling(上取樣)[9]。
-----
◎ Up Sampling(上取樣)
-----
由於只以最後一層的特徵圖,輪廓很模糊,所以上取樣兩次,以這三張圖加總,可以得到較清晰的輪廓。論文所做的實驗,繼續上取樣,結果不會比較好,所以上取樣只做兩次。
有關 FCN 較新的研究,可以參考 [20]。
-----
五、YOLOv1
-----
Fig. 20. Object Detection(物件偵測)[10]。
-----
◎ Object Detection(物件偵測)
-----
一般 CNN 是辨識一張圖片的類別。Object Detection 則是可以辨識圖片內的多個物件。
以 YOLOv1 為例,他把圖片先分成 7x7 個小框框,每個小框框可以預測兩張圖(中心落在框框內),這樣最多可以預測出 98 張圖。圖二十預測了狗、腳踏車跟汽車三個物件。
-----
Fig. 21. YOLO(你只要看一次)[10]。
-----
◎ YOLO(你只能看一次)
-----
圖廿一是 YOLOv1 的網路架構,最右邊是重點,輸出是 7x7x30。
也就是 49 個小框框,每個小框框預測兩張圖。每個圖有 15 個資訊,參考下一張圖的損失函數。
-----
Fig. 22. Loss Function(YOLO 的損失函數)[10]。
-----
◎ Loss Function(YOLO 的損失函數)
-----
S × S × (B * 5 + C) tensors。
S = 7。
B = 2。
C = 20。
S = 7,7 X 7 個預測框。B = 2,每個框預測 2 個物件(屬於同一種類別)。5 分別是中心 (x, y) 與寬高 w, h,以及是物件或不是物件。然後 C = 20 是這兩個物件屬於二十種類別的 confidences。
-----
有關更多 Object Detection,可以參考 [21]。
另外補充一下,你大概可以說,YOLOv3 = YOLOv1 + ResNet + FPN,而 FPN 跟 FCN 都使用最後三層特徵圖輔助運算。
-----
六、LSTM(Long Short-Term Memory)
-----
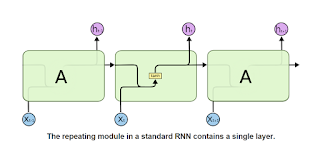
Fig. 23. RNN(遞迴神經網路)[11]。
-----
◎ RNN(遞迴神經網路)
-----
圖廿三是三個陽春的 RNN 單元,輸入與前一個輸出加總後,通過 tanh 再輸出。由於是時間序列,因此適合處理 speech、audio、video、text 等資料。如果你把 RNN旋轉九十度,那其實是一個很深的網路,只是每層都有輸入與輸出,不像一般 CNN,輸入跟輸出都只有一層。
-----
Fig. 24. LSTM(長的短期記憶)[11]。
-----
◎ LSTM(長的短期記憶)
-----
RNN 由於有梯度消失 [7] 與梯度爆炸 [8] 等問題,因此後續又有學者提出 LSTM。大家看到 LSTM,有沒有想過,為何單元裡有三個 sigmoid 跟兩個 tanh?
其實 sigmoid 在這裡不是激活函數,而是當作類比的閘門,用來控制輸入的百分比在 0 與 1 之間,所以後續又執行乘法。至於 tanh 有兩個,只要看一下圖廿四就知道,加總後要再經過一個非線性的激活函數,進行非線性轉換,增加模型的表現能力。簡單來說,就是兩層的意思。
LSTM 之外,也有 GRU 單元,架構簡化而效能接近。
-----
七、Seq2seq(Sequence to Sequence)
-----
Fig. 25. Seq2seq(序列到序列)[12]。
-----
◎ Seq2seq(序列到序列)
-----
Sequence to sequence,以翻譯為例,左邊的輸入是一個英文句子,右邊的輸出是一個對應的德文句子。先把英文句子轉成向量 [22] 輸入,壓縮成單一向量,再把向量解碼成德文。
這個架構也可以執行摘要的功能。只要把(英文、德文)換成(全文、摘要)即可!
-----
八、Attention
-----
Fig. 26. Attention(注意力)[13]。
-----
◎ Attention(注意力)
-----
Seq2seq 的單一向量儲存空間有限,會損失資訊。因此 Attention 把左邊的句子壓縮成多向量,每個向量有不同的權重,權重如何得到?靠訓練。
-----
九、ConvS2S(Convolutional Seq2seq)
-----
Fig. 27. ConvS2S(卷積的序列到序列)[14]。
-----
◎ ConvS2S(卷積的序列到序列)
-----
ConvS2S 跟下一個 Transformer 都屬於 STORM 的架構,Source Target Output Relational Model。只是 ConvS2S 使用一維的 convolution 代替 LSTM / GRU,而 Transformer 則以 self-attention 的架構,RNN 跟 CNN 都不使用。但讀者可以注意到 Transformer 裡面還是有用到 FNN 的神經網路用來升降維。
讀者若能徹底掌握 Transformer,則 ConvS2S 很容易從 Transformer 推演過來。
-----
十、Transformer
-----
Fig. 28. Transformer(變形金剛)[15]。
-----
◎ Transformer(變形金剛)
-----
以下以英德翻譯為例,右邊 Stage3 是全部的核心。
訓練時 Qd 找到編碼端的 Ke、Ve,也找到 解碼端的 Kd、Vd,對齊後輸出需要的德文。
測試時 Qd 找到編碼端的 Ke、Ve,透過訓練好的權重,直接輸出需要的德文。
-----
圖廿八對第一次看的人應該很複雜,不過整個 Transformer 的架構確實就是如此。
分成十小節說明:
一、I/O Embedding
Word2Vec。Stage1 不管 Encoder 端的英文或者 Decoder 端的德文,都先從 one-hot 編碼轉成詞向量 [22]。
二、Positional Encoding
公式跟跟訓練結果差不多,用公式。
三、Attention
Query、Key、Value。詞向量再分解成 Q、K、V。如何分解?靠訓練出來的權重矩陣。
四、Multi-Head
套用 CNN 多個卷積核 的概念讓結果變好。
五、Masked
保持 Auto Regression,output 不考慮 i 之後字的因素。
六、Skip
ResNet(Dropout)[6]。
七、Layer Normalization
BN 每筆資料每層的某個位置正規化,LN 某筆資料某層的所有位置正規化,正規化 - 減 mean 再除以 STD [19]。
八、FNN
調整輸出跟輸入的維度 [5]。
九、Linear
打分數。
十、Softmax
是 Logistic Regression 的推廣,
資料為 0 ~ 1 之間,總和為 1 的離散機率分布。
-----
Fig. 29. Query、Key、Value [15]。
-----
◎ Query、Key、Value
-----
首先透過權重矩陣把已經 embed 好的詞向量轉成 Q、K、V 三個分量。Q 跟 K 其實差不多,但概念上 Q 是變數,K 是常數,K 是位址的概念,V 是內容的概念。Qd 可以分別對應到 Ke 跟 Kd,這樣運算起來比較方便。
-----
Fig. 30. Self Attention(自注意力)[15]。
-----
◎ Self Attention(自注意力)
-----
QKV:
QK 對齊(內積、餘弦相似)。(如果 LSTM 的 Attention 的話,是加法)。
Root of dk:
dk:dimension of K,避免向量的分量值透過 Logistic Regression 後都是 1 或者都是 0,造成無 attention。
-----
Fig. 31. Qd、Ke、Ve(編碼端的 QKV)[15]。
-----
◎ Qd、Ke、Ve(編碼端的 QKV)
-----
Qd 找到 Ke、Ve,編碼端的英文。
-----
Fig. 32. Qd、Kd、Vd(解碼端的 QKV)[15]。
-----
◎ Qd、Kd、Vd(解碼端的 QKV)
-----
Qd 找到 Kd、Vd,解碼端的德文。
-----
Conclusion
本文簡單介紹了五篇 CV 跟五篇 NLP 最重要的論文。讀者若希望有進一步的認識,CV [25] 跟 NLP [29] 都有更多介紹!
-----
演講公告
8 月 25 日 星期日 下午兩點到五點,清大圖書館一樓清沙龍。
8 月 24 日 星期六 下午兩點到五點,北科大第六教學大樓,一樓開放空間。
6 月 15 日 星期六 下午兩點到五點,北科大綜合科館地下一樓 B08。
5 月 25 日 星期六 下午兩點到五點,清大風雲樓二樓靠門口處。
5 月 18 日 星期六 下午兩點到五點,開南大學卓越樓 621 室。
5 月 9 日 星期四 下午兩點二十到四點,台大明達館 223 室。
-----
全方位 AI 課程(六十小時搞定深度學習)
https://hemingwang.blogspot.com/2019/10/preface.html
-----
References
[1] 深入淺出 Deep Learning(四):CNN
http://hemingwang.blogspot.com/2018/02/deep-learningcnn.html
[2]深入淺出 Deep Learning(二):LeNet & BP
http://hemingwang.blogspot.com/2018/02/deep-learninglenet-bp.html
[3] AI從頭學(九):Back Propagation
http://hemingwang.blogspot.tw/2017/02/aiback-propagation.html
[4] Math(五):Manifold
http://hemingwang.blogspot.com/2019/04/mathmanifold.html
[5] AI從頭學(二八):Network in Network
http://hemingwang.blogspot.com/2017/06/ainetwork-in-network.html
[6] AI從頭學(三三):ResNet
http://hemingwang.blogspot.com/2018/09/airesnet.html
[7] Vanishing Gradient
http://hemingwang.blogspot.com/2019/05/vanishing-gradient.html
[8] Exploding Gradient
http://hemingwang.blogspot.com/2019/05/exploding-gradient.html
[9] AI從頭學(三四):FCN
http://hemingwang.blogspot.com/2018/02/deep-learningfcn.html
[10] AI從頭學(三六):YOLO v1
http://hemingwang.blogspot.com/2018/04/deep-learningyolo-v1.html
[11] NLP(一):LSTM
http://hemingwang.blogspot.com/2019/09/lstm.html
[12] NLP(二):Sequence to Sequence
http://hemingwang.blogspot.com/2019/09/seq2seq.html
[13] NLP(三):Attention
http://hemingwang.blogspot.com/2019/01/attention.html
[14] NLP(四):ConvS2S
https://hemingwang.blogspot.com/2019/04/convs2s.html
[15] NLP(五):Transformer
http://hemingwang.blogspot.com/2019/01/transformer.html
[16] NLP(六):BERT Overview
https://hemingwang.blogspot.com/2019/01/bert-overview.html
-----
[17] An overview of gradient descent optimization algorithms
http://ruder.io/optimizing-gradient-descent/
[18] An Overview of Regularization Techniques in Deep Learning (with Python code)
https://www.analyticsvidhya.com/blog/2018/04/fundamentals-deep-learning-regularization-techniques/
[19] 深度学习中的Normalization模型 - 知乎
https://zhuanlan.zhihu.com/p/43200897
[20] 深度学习(十九)——FCN, SegNet, DeconvNet, DeepLab, ENet, GCN - antkillerfarm的专栏 - CSDN博客
https://blog.csdn.net/antkillerfarm/article/details/79524417
[21] 關於影像辨識,所有你應該知道的深度學習模型 - Steven Shen - Medium
https://medium.com/@syshen/%E7%89%A9%E9%AB%94%E5%81%B5%E6%B8%AC-object-detection-740096ec4540
[22] [NLP] 秒懂词向量Word2vec的本质 - 知乎
https://zhuanlan.zhihu.com/p/26306795
-----
[23] AI從頭學(目錄)
http://hemingwang.blogspot.com/2016/12/ai_20.html
[24] LeNet Lab(目錄)
https://hemingwang.blogspot.com/2019/04/lenet-lab.html
[25] 30 Topics for Deep Learning
http://hemingwang.blogspot.com/2019/04/30-topics-for-deep-learning.html
[26] Machine Learning
https://hemingwang.blogspot.com/2019/04/machine-learning.html
[27] Mathematics
https://hemingwang.blogspot.com/2019/04/mathematics.html
[28] Deep Learning Highlight
http://hemingwang.blogspot.com/2019/02/deep-learning-highlight.html
[29] AI Seminar(目錄)
https://hemingwang.blogspot.com/2019/01/ai-seminar.html































No comments:
Post a Comment