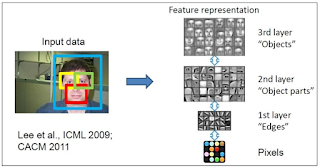
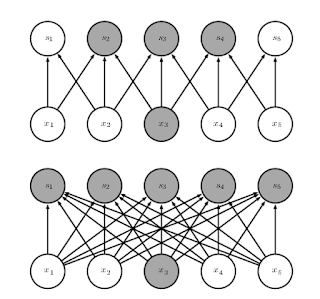
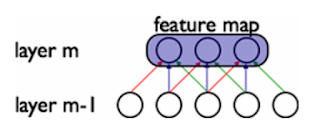
AI 從頭學(一三):LeNet - F6
2017/03/08
前言:
在上一篇中,LeNet-5 用的 convolution 跟 sub-sampling 的 filters 並沒找出,但原理應該已經講得很清楚了。本篇繼續 MLP 的部分。首先從 F6 開始,接下來會有 RBF 跟 Cost function。
-----
Fig. Net(圖片來源:
Pixabay)。
-----
Summary:
本文主要探討 LeNet 背後設計原理的由來。另外,在空間的 Convolutional Neural Network(CNN)與時間的 Recurrent Neural Network(RNN)之後,是否神經網路也能有更「智慧」的表現,例如「模仿」,在文末會簡單討論。
羅馬不是一天造成的,1998 年發表的 LeNet [1] 也不是一天造成的 [2]-[4]。早在 1983 年,Fukushima [4] 的論文中,LeNet 的概念已相當完整,只可惜還沒加上 Back Propagation (BP) [5],因為 BP 這時也才剛被世人所知 [6]-[8]。
LeNet 最後三層是全連接、傳統的類神經網路。在 F6 這一層中,主要探討 activation function [9]-[14] 中的 tanh,深入的討論 [15] 放在 Appendix A中 [1],作者把這一段放在Appendix 有其道理,因為 convergence [16], [17] 需要另外討論,並不是本文小小的篇幅所能容納。
Convergence,在 RNN 中更加重要 [18]-[20],因為梯度過於陡峭或平滑都會造成難以收斂,後來發展的 Long Short-Term Memory(LSTM)[21] 有效地改善此現象。而 Dropout [22], [23] 藉著隨機丟棄神經元連結的方法,有效地改進 overfitting 的問題。若要模仿大腦運作的方式,也許可以引進 Mirror Neuron System(MNS)的概念 [24]-[28]。
-----
Questions
Q1:3 layers
Q2:Back propagation
Q3:Activation function
Q4:Convergence
Q5:Overfitting and dropout
Q6:Mirror neurons
-----
Q1:3 layers
第一個問題是:全連接層,為何要設成三層,答案是:不一定。
圖1a 的 LeNet-5 全連接層是三層。圖1b 是類似的架構。圖1c、1d 則可說是全連接層的嘗試。參考圖1e,兩層的話效能不佳,三層以上就好些,當然更多層效能更好。
由於 LeNet-5 有多層的 convolution 與 sub-sampling layers,所以全連接層雖然只有三層,效能還是很好。輸入端這幾層的概念,來自 Fukushima,參考圖1f、1g、1h、1i。只是 Fukushima 並未導入 BP,因此效能不佳,參考圖2f,連簡單的 5 都會識別錯誤。
較完整的作法,是 convoluton + sub-sampling + BP,可以識別較複雜的數字,參考圖2a、2c。如果缺 convolution 或 BP,則只能識別較無變化的數字,如圖2d、2e。
-----
圖一:
Fig. 1a. Last 3 Layers [1]。
Fig. 1b. Convolutional parts [2]。
Fig. 1c. Full connected parts, Net-1 to Net-3 [3]。
Fig. 1d. Full connected parts, Net-4 and Net-5 [3]。
Fig. 1e. Nets, full connected parts, comparison of performance [3]。
Fig. 1f. Neocognitron, simple, complex, and hypercomplex cells [4]。
Fig. 1g. Neocognitron, convolutional structures [4]。
Fig. 1h. Neocognitron, sparse connection [4]。
Fig. 1i. Neocognitron, activation function [4]。
-----
圖二:
Fig. 2a. LeNet-5, inputs [1]。
Fig. 2b. Initial parameters of the output RBFs [1]。
Fig. 2c. Zip codes [2]。
Fig. 2d. Nets, inputs [3]。
Fig. 2e. Neocognitron, inputs [4]。
Fig. 2f. Neocognitron, weak performance [4]。
-----
Q2:Back propagation
問題二,為何 Fukushima 不用 BP [7], [8],答案是,當時 BP 還不流行 [5], [6]。
"To my knowledge, the first NN-specific application of efficient BP as above was described in 1981 (Werbos, 1981, 2006). Related work was published several years later (LeCun, 1985, 1988; Parker, 1985), p. 91." [6].
Fukushima 這篇是 1983 年發表,根據上文,BP 在 1981 才正式用在 NN,以當時資訊的流通程度,嗯。所以我們大概可以說:
Fukushima + Werbos = LeCun。
-----
Q3:Activation function
F6 這一層,在論文中,重心放在為何要使用 tanh,而且是放在附錄中 [1]。圖3a 是論文用的 activation function。參考圖3b、3c,比起 sigmoid,tanh 是好一點,不過後來,其實也不能說後來,因為早在 Fukushima,就用過ReLU,參考圖1i。ReLU [12], [13] 之外,也有更新的 maxout [14]。所以究竟要簡單瞭解一下 tanh,還是要深入探討,從 fixed point [15] 挖下去,我想先不要挖比較保險。因為這牽涉到問題四,convergence 是個大問題。
"Usually, the parameters in the linear components are learned to fit the data, while the nonlinearities are pre-specified to be a
logistic,
tanh,
rectified linear, or
max-pooling function." [11].
"The
rectified linear activation function (Jarrett et al., 2009; Glorot et al., 2011), which does not saturate like sigmoidal functions, has made it easier to quickly train deep neural networks by alleviating the difficulties of weight-initialization and vanishing gradients. Another recent innovation is the “
maxout”
activation function, which has achieved
state-of-the-art performance on multiple machine learning benchmarks (Goodfellow et al., 2013)" [11].
在 [10] 中提到 ReLU 比較好,上面的 [11] 則告訴大家,也要多注意 maxout 這個較新的 activation function。至於簡單的比較,則放在 [9]。
F6 到 F7 這一層並沒有用 tanh,而是用 RBF,參考圖3d,這跟 LeNet-5 主要想處理 ASCII 有關。經過了 ASCII 的濾波器,參考圖2b,我們可以看到圖2a 的 F6 層已經跟 ASCII 很像,這時再使用 RBF 轉到 F7 的輸出層就順理成章了。有關 RBF,之後有時間再討論。
圖四1a 跟 1b 分別是 [1] 跟 [3] 的 cost function,可看出這兩篇論文有相關性。[3] 並沒用 RBF,因為 [3] 的原始輸入已經跟 [1] 的 C5 層很接近(我猜的),所以 [3] 就直接進全連接層了。有關 cost function,之後有時間再討論。
-----
圖三:
Fig. 3a. Activation function, Atanh(Sa) [1]。
Fig. 3b. Activation function, tanh(x) [9]。
Fig. 3c. Activation function, graph of tanh(x) [9]。
Fig. 3d. RBF, Radial basis function [1]。
-----
圖四:
Fig. 4a. Cost function [1]。
Fig. 4b. Cost function [3]。
-----
Q4:Convergence
F6 這一層主要是討論 tanh 的 convergence。有種種方法可以改進 neural networks 的 convergence [16], [17]。這個 issue 在 RNN 中更顯重要 [18]-[20],後來 Hochreiter 跟 Schmidhuber 提出 LSTM [21] 的模型來改善 RNN 不易收斂的問題。無論如何,這個問題更大、更基本,已超出本文的篇幅,以及作者現階段的能力了。
-----
Q5:Overfitting and dropout
"Large networks are also slow to use, making it difficult to deal with
overfitting by combining the predictions of many different large neural
nets at test time. Dropout is a technique for addressing this problem.
The key idea is to randomly drop units (along with their connections)
from the neural network during training. This prevents units from
co-adapting too much." [23].
Convergence 是效能的議題,Overfitting 也是效能的議題。所謂 Overfitting,簡單說,就是考古題做的好,真的到考場,表現卻不佳。訓練好,測試不佳,遑論應用。
"When training with Dropout, a randomly selected subset of activations
are set to zero within each layer. DropConnect instead sets a randomly
selected subset of weights within the network to zero. Each unit thus
receives input from a random subset of units in the previous layer." [22].
Dropout 是用來解決 overfitting 的方法之一 [23]。把 dropout 一般化,則是 dropconnect [22]。事實上,dropout [23] 跟 maxout [14] 是一組的,藉著隨機丟棄神經元的方式簡化網路,改進效能,參考圖5。這方法已經跟真實的腦神經在使用中減少不必要的連結以強化某項功能很接近,只是,隨機?真的會好嗎?還是,不應該隨機,而是要找出某種更像大腦真實運作的方法呢?
跟 convergence一樣,overfitting 也超出本文範圍了。
-----
圖五:
Fig. 5. Dropout [23]。
-----
Q6:Mirror neurons
我是很驚訝 dropout 這麼晚才被提出,因為腦神經科學的研究已經很久了。我才剛接觸 deep learning(DL),就想到這個點子,然後就發現 dropout 已經有人做了。我認為 mirror neurons 的概念或許有助於 DL 往真正的人工智慧,也就是 Strong AI 前進。
有關運動神經元,我也沒去找最新的研究來看,只是先就之前的論文資料庫中剪一些讀者可能會感興趣的部分,參考圖6a、6b、6c、6d。就我浮面的瞭解,目前 DL 應該是還沒有人往這方向邁進。
鏡像神經元主司模仿,「其發現始於 1992,迪⋅派勒吉諾,發現猴子的 F5 神經元,不只會在猴子本身抓香蕉時活化,也會在猴子看到其他人/猴子抓香蕉時活化。然後再經過四年,里佐拉蒂的研究團隊不斷重複檢測該實驗結果,才在 1996 年正式用“鏡像神經元"發表在 Brain 和 Cognitive Brain Research等國際知名期刊中,開啟鏡像神經元之於認知神經科學的世紀革命。」[26]。
「而人類大腦的鏡像神經系統,已知包括前運動皮質之腹側(或布洛卡區)(ventral premotor cortex)、頂葉下側小葉(inferior parietal lobule)、前扣帶迴皮質(anterior cingulated cortex)、及腦島(insula) 」[26]。
「從神經解剖學的觀點來看,被某些學者歸類為「情感型鏡像神經元系統」(affective mirror neuron system)的腦島前區與前扣帶回(anterior cingulate)裡面,確實有些較特別的神經元,伸出了長長的軸突,將前額葉、顳葉、邊緣系統緊密相連,讓它們之間的訊息傳遞更為快捷、直接,這種神經元稱為 spindle neuron(von Economo neuron)」 [28]。
「大翅鯨、大猩猩與黑猩猩跟人類一樣,在情感型鏡像神經元系統中都有 spindle neuron 作為聯繫運動、知覺、情感的樞紐。音樂與語言的相似性與相異性,在音樂學領域中已有許多討論,然而從生物演化的角度來看,這兩者都應該被納入更廣泛、更原始的「運動功能」中重新思考。從鏡像神經元的觀點來解釋音樂認知,可能還需要結合動作科學(movement science)與有關小腦的知識,此一理論才能夠趨於完備」 [28]。
-----
圖六:
Fig. 6a. Lateral view of the monkey brain showing [24]。
“In color, the motor areas of the frontal lobe and the areas of the posterior parietal cortex. For nomenclature and definition of frontal motor areas (F1–F7) and posterior parietal areas (PE, PEc, PF, PFG, PG, PF op, PG op, and Opt) see Rizzolatti et al. (1998). AI, inferior arcuate sulcus; AS, superior arcuate sulcus; C, central sulcus; L, lateral fissure; Lu, lunate sulcus; P, principal sulcus; POs, parieto-occipital sulcus; STS, superior temporal sulcus.” [24].
Fig. 6b. Mirror neuron system [25]。
“Neural mechanisms of imitation. Shown is a representation of the core circuitry for imitation on the lateral wall of the right cerebral hemisphere, together with the internal models the circuitry implements during imitation. Abbreviations: MNS, mirror neuron system; STS, superior temporal sulcus.” [25].
Fig. 6c. Neural mechanisms of imitative learning and social mirroring [25]。
“In this model, imitative learning is implemented by interactions among the core imitation circuit, the dorsolateral prefrontal cortex (BA46) and a set of areas relevant to motor preparation (PMd, pre-SMA, SPL), whereas social mirroring is implemented by the interactions among the core imitation circuit, the insula and the limbic system. Abbreviations: BA46, Brodmann area 46; MNS, mirror neuron system; PMd, dorsal premotor cortex; pre-SMA, pre-supplementary motor area; SPL, superior parietal lobule STS, superior temporal sulcus.” [25].
Fig. 6d. Mirror neuron system and music [28]。
-----
結論:
從 LeNet-5 這個 CNN 的全連接層,討論到 activation function 的 convergence,到 overfitting、dropout、以及 mirron neurons,本次提出的問題多於回答的問題。未來問題只有越來越多越難,回答只有越來越慢越辛苦。然而,每回答出一個問題,總是令人雀躍、萬分喜悅的。
大家一起加油吧!
-----
補充:
看起來 DL 跟 MNS 有一起被探討,但是在 DL 圈尚未應用這個概念去開發 Nets [29]-[31]。
-----
出版說明:
2019/09/24
本篇是剛接觸深度學習時的筆記。限於當時的能力,無法進行深入的討論,不過找了一些歷史文件,還是有一些價值。人工智慧、認知科學、腦科學三者的交集被歸於智能科學,而深度學習是人工智慧的一支,所以本文也涉及了一點點腦科學的討論。
-----
References
[1] 1998_Gradient-Based Learning Applied to Document Recognition
[2] 1989_Backpropagation applied to handwritten zip code recognition
[3] 1989_Generalization and network design strategies
[4] 1983_Neocognitron, a neural network model for a mechanism of visual pattern recognition
[5] 反向傳播算法 - 維基百科,自由的百科全書
https://zh.wikipedia.org/wiki/%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD%E7%AE%97%E6%B3%95
[6] 2015_Deep learning in neural networks, An overview
[7] 1990_30 years of adaptive neural networks, perceptron, madaline, and backpropagation
[8] 1989_Theory of the backpropagation neural network
[9]Google軟件工程師解讀:深度學習的activation function哪家強?_幫趣網
http://bangqu.com/gpu/blog/5484
[10] 2015_Deep learning
[11] 2014_Learning activation functions to improve deep neural networks
[12] 2015_Delving deep into rectifiers, Surpassing human-level performance on imagenet classification
[13] 2010_Rectified linear units improve restricted boltzmann machines
[14] 2013_Maxout networks
[15] Fixed point (mathematics) - Wikipedia
https://en.wikipedia.org/wiki/Fixed_point_%28mathematics%29
[16] 1992_First-and second-order methods, for learning between steepest descent and Newton's method
[17] 1988_Improving the convergence of back-propagation learning with second order methods
[18] 1990_Backpropagation through time, what it does and how to do it
[19] 1994_Learning long-term dependencies with gradient descent is difficult
[20] 1996_Learning long-term dependencies is not as difficult with NARX recurrent neural networks
[21] 1997_Long short-term memory
[22] 2013_Regularization of neural networks using dropconnect
[23] 2014_Dropout, a simple way to prevent neural networks from overfitting
[24] 2004_The Mirror-Neuron System
[25] 2005_Neural mechanisms of imitation
[26] 2006_自閉症的破鏡之旅_鏡像神經元
http://beaver.ncnu.edu.tw/projects/emag/article/200704/%A6%DB%B3%AC%AFg.pdf
[27] 2006_Music and mirror neurons, from motion to 'e'motion
[28] 2008_音樂與鏡像神經元:從運動到情緒
http://1www.tnua.edu.tw/~TNUA_MUSIC/files/archive/49_5c388dc4.pdf
[29] 2017_Is Spoken Language All-or-Nothing, Implications for Future Speech-Based Human-Machine Interaction
[30] 2016_Neural Information Processing in Cognition, We Start to Understand the Orchestra, but Where is the Conductor
[31] 2016_Motor development facilitates the prediction of others' actions through sensorimotor predictive learning